New
Nov 17, 2020 6:08 AM
#51
| Every couple of years, when this stuff resurfaces with different numbers, everyone has the same exact debates over it. So far, it has never been decisive, so, unless 2020 decoded to glitch the matrix, I don't see why it would change. The solution is to use brackets smarter. Moral of the story: don't note implied multiplication after a division without using brackets to signal the result that you want. |
KosmonautNov 17, 2020 6:19 AM
 |
Nov 17, 2020 6:10 AM
#52
Darius said: deg said: fsharp_asharp said: 6 ÷ [2 x (1+2)] ah yep that how you do it im just curious on the 1 answer and the rule that says M is process first before D because thats what i clearly remember getting at school but apparently im having false memory of that i got 9 when i go like this (6/2) (1+2) and thats what my original answer is and what i voted for M over D is old stuff from 1917. And we were all probably taught that because our teachers were taught like that but it's not how you should do it nowadays. Don't trust the boomers... So, the answer is still 9, lol. Type it in wolfram or something... lol you got me im like part of the boomer generation anyway |
Nov 17, 2020 6:13 AM
#53
| @deg Yes, if it were not for that misleading visual thing, that's how you'd calculate it and it the answer would be 9. Multiplication and division are actually the same thing, it's just that division by a number d is just multiplication by the fraction 1/d, so they have the exact same rank when it comes to precedence. That division sign is a bit antiquated from my point of view. And, in the end, the question is one of attention, not of actual mathematics. |
Nov 17, 2020 6:18 AM
#54
It does not, but apparently some people choose to believe this. Don't ask me why, I only use fractions when writing a division and I find no ambiguity in it. |
Nov 17, 2020 6:18 AM
#55
| The wrong answer is answering it, and it bewilders me that so many still fall for it.. |
Nov 17, 2020 6:25 AM
#56
| It´s 1, you should solve the operations with () first |
| "If I get reincarnated… I wanna become a clam.” – Monkey D Luffy |
Nov 17, 2020 8:50 AM
#57
| Let me try in postfix again: 6/2 (1+2)= 6 2 / 1 2 + * 1) Divide the first number by the second number and save the result as "r1": 3 2) Add the two numbers after the division mark and save the result as "r2": 3 3) Multiply r1 with r2 and store the result as "rfinal" 4) Display "rfinal": 9 |
Nov 17, 2020 9:08 AM
#58
| It’s 9. The fact that there’s such heated debate over this is hilarious. I get how people interpret it as 1, but not anything else lol. Yes, according to PEMDAS, things inside of a parentheses take precedent. But, the 2 isn’t inside a parentheses so you wouldn’t distribute it first if there’s a multiplication or division sign already in front of it. 6 ÷ 2(1+2) Technically, you’d add 1+2 to get 3, then divide 6/2 to get 3 and finally multiple 3x3 to get 9. It would be 1 if it were written like this since the 2 is now inside a parentheses. 6 ÷ (2(1+2)) I pretty sure a lot people get it wrong because the problem is notated too vaguely. |
EightSevenNov 17, 2020 9:41 AM
Nov 17, 2020 9:29 AM
#59
| 1 I can see how people interpret it if the equation was (6÷2)(1+2)=9 But since the equation is like that then there can be 2 interpretation Either A 6 ---(1+2) 2 =9 Or B 6 --- 2(2+1) =1 C? 6(2+1) --- 2 =9 B looks more logical to me so 1 |
| "Rating are for Casul" "While masterpiece are for Pleb" "But shit taste is enlightenment" "Go watch School Days you Weebs" |
Nov 17, 2020 9:52 AM
#60
| Many people have already answered correctly with great explanations, but I would like to show a different way of writing it to help others understand. So, the most common reasoning for the answer [b]1[b] is because of the order of operations (or PEMDAS or whatever thing you learned). However, using that actually shows that the answer is 9: 6÷2(1+2) First off, you solve for what is inside the brackets. Most people actually got this step right. 6÷2(3) Now here comes the part where most people are likely to mess up. Some people are tempted to multiply 2 with 3. However, that shouldn't be the case, as 2 is NOT inside the brackets. Therefore, it is not part of the "bracket/parentheses" part of the order of operations. A good way to avoid this mistake is that, once you have only one value inside the brackets, simply remove them. And when you remove brackets, it simply becomes a multiplication, like this: 6÷2×3 Afterwards, the standard order of operations can be used: 6÷2=3 3×3=9 Therefore, the answer is 9. Another way to avoid making these types of mistakes is by simply removing divisions altogether. When you divide a number by two, it is essentially the same thing as multiplying it by 0.5 or ½. As such, simply replace ÷2 with a multiplication, being either ×0.5 or ×½. 6÷2(1+2)=6×½(1+2)=6×½(3) Also, if it helps, you can also put 6/1 and 3/1, to avoid making any calculation errors and to put everything into one fraction, which makes it easier to visualize if you are not the greatest at math.  From here on out, it's pretty straightforward: solve for the numerator and the denominator, and then divide these two by each other: 6×1×3=18 1×2×1=2 18÷2=9 Therefore, using this method as well, the answer is 9. That's pretty much it. If someone disagrees with me, I'd love to see their perspective on this equation. |
Nov 17, 2020 9:59 AM
#61
deg said: @_Mataga_ @Darius @Kosmonaut i found this on the twitter post @Oeufhbpi posted https://en.wikipedia.org/wiki/Order_of_operations#Mixed_division_and_multiplication it says there that in cases of 1/2x then M is process first before D 6/2x3 6/6 1 so ye its still 1? or PEMDAS is still the best? lol The paragraph states With this interpretation 1 ÷ 2x is equal to (1 ÷ 2)x. However, in some of the academic literature, multiplication denoted by juxtaposition (also known as implied multiplication) is interpreted as having higher precedence than division, so that 1 ÷ 2x equals 1 ÷ (2x), not (1 ÷ 2)x. For example, the manuscript submission instructions for the Physical Review journals state that multiplication is of higher precedence than division with a slash, and this is also the convention observed in prominent physics textbooks such as the Course of Theoretical Physics by Landau and Lifshitz and the Feynman Lectures on Physics. This means some academic journals specifically use, as guidelines or submission instructions for the papers, that M should precede over D to clear any ambiguity, not that it's universally agreed upon. In other words, something like Ω/2Δ in a paper should be interpreted as (Ω) ÷ (2Δ) and the authors submitting to those journals should follow the established formatting when writing their paper for that specific journal. Naturally to make it universally unambiguous, one would write Ω/(2Δ). |
Nov 17, 2020 10:56 AM
#62
| Okay, first of all, why use a colon instead of any other operator? A colon is supposed to be for ratios! Well, ratios are like fractions anyway, so I'll accept it. The equation itself is faulty to the point that many people misinterpreted it. It shouldn't be written like that. My initial answer is one, then I also see where nine comes from, and it's more logical like that. However, like I said earlier, the equation should not be written like that. You can write 6/(2(1+2)) or (6/2)(1+2) and the answers will come out easily. |
Nov 17, 2020 3:08 PM
#63
deg said: Kosmonaut said: deg said: Oeufhbpi said: 149597871 said: Oeufhbpi said: 149597871 said: Peaceful_Critic said: I could be wrong, but I think it's 7. Distributive property 2(1+2) 2 times 1 =2 2 times 2=4 Then according to PEMDAS, you then divide 6 divide 2+4 6 divided by 2=3 3+4=7 You are wrong, terribly wrong. I came back after more than a month and you greet me this? You should be ashamed of yourself. On a side note, I know this one is quite old, but it's funny how every year we get these "viral" math problems that are pretty much the same but with different numbers. Anyway, the correct answer is 9. My math still sucks, of course, but honestly, at least try something new and original. Wait lol, all of that only to get the answer wrong yourself. The answer is 1, at least that's what Matt Parker says. I don't even know who this guy is but in most countries, the answer has been 9 for at least a century or so. 6/2(1+2) = 9 6/(2(1+2)) = 1 Anyway, see you all next week, or month, or year. He's a famous math guy. I trust his reasoning (though admittedly I don't really understand why it couldn't be 9). Here's his full response: https://twitter.com/standupmaths/status/1327563739290333184 yep implied multiplication it is then to get the answer of 1 6/2(1+2) 6/2(3) 6/6 1 it still follows PEMDAS @Kosmonaut here is my take to get that 1 answer that it follows PEMDAS still we need @Meusnier on this thread lol @Kosmonaut @AlexPaulLEWZ Just quoting those who said interesting things. PEMDAS, DMAS, BIDMAS, BODMAS, all this nonsense is still taught these days? The answer was in the question. The notation is wrong and what is written is meaningless. Amusing to see people insulting each other about something they are manifestly clueless about. As Alex said, you can only write 6/(2(1+2)) or (6/2)(1+2), and 6/2(1+2) is incorrect. People argue over left versus right, or division against multiplication, but multiplication and division is the same thing, and the multiplication is commutative, that is: a ⋅ b=b ⋅ a. Besides schoolboys, no one writes /, unless someone writes 1/3 or f/g, with f,g two given functions. The solution to avoid confusion is to add the exponent -1 for the inverse, and to always write expressions of the form: 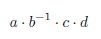 and never expressions of the following form:  This is not about being pedantic, all signs have a meaning, and if one is missing, the entire expression may stop to make sense; by the way, this is exactly the same thing to leave the possibility of distinct explanations for the reader and being meaningless. Using calculators and computers has nothing to do with the argument here as they are designed to satisfy some arbitrary conventions. They do not constitute anything reliable. Rather than believing inept teachers, one should rather look back at the axioms of fields. Those are sets X equipped with too operations, + and ⋅, for which there exists distinct elements 0, 1∈X, such that x+0=x and x ⋅ 1=x for all x∈X, and such that for all for all x∈X, there exists y∈X such that x+y=0. We note y=-x. We also require that for all x∈X different from 0, there exists y∈X such that x ⋅ y=1. We write  . .Then the only axioms satisfied by the field X are the following :
In particular, there is nothing saying you should compute anything from left to right or right to left. One has to make a difference between an inconvenient rule taught to children so that they make less computational mistakes and what one can actually rightfully do according to the axioms. @Kosmonaut Feel free to call me Neo from now. Now we all know what is being redpilled, it means being able to understand basic mathematical axioms. @Phloup Needless to say, I disagree with your post. |
Nov 17, 2020 3:34 PM
#64
Meusnier said: I see, admittedly I'm not big on mathematics, because my subject path in school wasn't focused on it. So, if I understood it correctly, I was off for thinking the equation was written 'right' and that it meant something. I thought it lacked further notation, like more brackets, to at least clear the ambiguity, but I didn't think it was completely invalid without them. An ambiguous text still has meaning and its meaning is being ambiguous. deg said: Kosmonaut said: deg said: I'm no mathematician. With the way my school taught math, 2(1+2) would only be a term if it was noted by adding even more brackets around it 6:[2(1+2)]. Without these, it would always be 9. Now, if mathematicians in academia automatically and obscurely consider it a term without any further notation, then I guess only they abide by it. Oeufhbpi said: 149597871 said: Oeufhbpi said: 149597871 said: Peaceful_Critic said: I could be wrong, but I think it's 7. Distributive property 2(1+2) 2 times 1 =2 2 times 2=4 Then according to PEMDAS, you then divide 6 divide 2+4 6 divided by 2=3 3+4=7 You are wrong, terribly wrong. I came back after more than a month and you greet me this? You should be ashamed of yourself. On a side note, I know this one is quite old, but it's funny how every year we get these "viral" math problems that are pretty much the same but with different numbers. Anyway, the correct answer is 9. My math still sucks, of course, but honestly, at least try something new and original. Wait lol, all of that only to get the answer wrong yourself. The answer is 1, at least that's what Matt Parker says. I don't even know who this guy is but in most countries, the answer has been 9 for at least a century or so. 6/2(1+2) = 9 6/(2(1+2)) = 1 Anyway, see you all next week, or month, or year. He's a famous math guy. I trust his reasoning (though admittedly I don't really understand why it couldn't be 9). Here's his full response: https://twitter.com/standupmaths/status/1327563739290333184 yep implied multiplication it is then to get the answer of 1 6/2(1+2) 6/2(3) 6/6 1 it still follows PEMDAS @Kosmonaut here is my take to get that 1 answer that it follows PEMDAS still we need @Meusnier on this thread lol @Kosmonaut @AlexPaulLEWZ Just quoting those who said interesting things. PEMDAS, DMAS, BIDMAS, BODMAS, all this nonsense is still taught these days? The answer was in the question. The notation is wrong and what is written is meaningless. Amusing to see people insulting each other about something they are manifestly clueless about. As Alex said, you can only write 6/(2(1+2)) or (6/2)(1+2), and 6/2(1+2) is incorrect. People argue over left versus right, or division against multiplication, but multiplication and division is the same thing, and the multiplication is commutative, that is: a ⋅ b=b ⋅ a. Besides schoolboys, no one writes /, unless someone writes 1/3 or f/g, with f,g two given functions. The solution to avoid confusion is to add the exponent -1 for the inverse, and to always write expressions of the form: 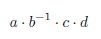 and never expressions of the following form:  This is not about being pedantic, all signs have a meaning, and if one is missing, the entire expression may stop to make sense; by the way, this is exactly the same thing to leave the possibility of distinct explanations for the reader and being meaningless. Using calculators and computers has nothing to do with the argument here as they are designed to satisfy some arbitrary conventions. They do not constitute anything reliable. Rather than believing inept teachers, one should rather look back at the axioms of fields. Those are sets X equipped with too operations, + and ⋅, for which there exists distinct elements 0, 1∈X, such that x+0=x and x ⋅ 1=x for all x∈X, and such that for all for all x∈X, there exists y∈X such that x+y=0. We note y=-x. We also require that for all x∈X different from 0, there exists y∈X such that x ⋅ y=1. We write  . .Then the only axioms satisfied by the field X are the following :
In particular, there is nothing saying you should compute anything from left to right or right to left. One has to make a difference between an inconvenient rule taught to children so that they make less computational mistakes and what one can actually rightfully do according to the axioms. @Kosmonaut Feel free to call me Neo from now. Now we all know what is being redpilled, it means being able to understand basic mathematical axioms. @Phloup Needless to say, I disagree with your post. Still, I can't help but feel like my high school math teacher would be proud of me for turning a division into a multiplication, after so many years, even if I was wrong. I'll take solace in the little redpills, while you've already become big pharma. |
KosmonautNov 17, 2020 3:40 PM
 |
Nov 17, 2020 3:40 PM
#65
| Nine... Solve the ones in the bracket first, then solve in order from left to right because division and multiplication are in the same level. |
 (っ◔◡◔)っ 𝓘 𝔀𝓲𝓼𝓱 𝔂𝓸𝓾 𝓪𝓵𝓵 𝓱𝓪𝓿𝓮 𝓪 𝔀𝓸𝓷𝓭𝓮𝓻𝓯𝓾𝓵 𝓭𝓪𝔂 ♥ |
Nov 17, 2020 3:49 PM
#66
Kosmonaut said: Meusnier said: I see, admittedly I'm not big on mathematics, because my subject path in school wasn't focused on it. So, if I understood it correctly, I was off for thinking the equation was written 'right' and that it meant something. I thought it lacked further notation, like more brackets, to at least clear the ambiguity, but I didn't think it was completely invalid without them. An ambiguous text still has meaning and its meaning is being ambiguous. deg said: Kosmonaut said: deg said: I'm no mathematician. With the way my school taught math, 2(1+2) would only be a term if it was noted by adding even more brackets around it 6:[2(1+2)]. Without these, it would always be 9. Now, if mathematicians in academia automatically and obscurely consider it a term without any further notation, then I guess only they abide by it. Oeufhbpi said: 149597871 said: Oeufhbpi said: 149597871 said: Peaceful_Critic said: I could be wrong, but I think it's 7. Distributive property 2(1+2) 2 times 1 =2 2 times 2=4 Then according to PEMDAS, you then divide 6 divide 2+4 6 divided by 2=3 3+4=7 You are wrong, terribly wrong. I came back after more than a month and you greet me this? You should be ashamed of yourself. On a side note, I know this one is quite old, but it's funny how every year we get these "viral" math problems that are pretty much the same but with different numbers. Anyway, the correct answer is 9. My math still sucks, of course, but honestly, at least try something new and original. Wait lol, all of that only to get the answer wrong yourself. The answer is 1, at least that's what Matt Parker says. I don't even know who this guy is but in most countries, the answer has been 9 for at least a century or so. 6/2(1+2) = 9 6/(2(1+2)) = 1 Anyway, see you all next week, or month, or year. He's a famous math guy. I trust his reasoning (though admittedly I don't really understand why it couldn't be 9). Here's his full response: https://twitter.com/standupmaths/status/1327563739290333184 yep implied multiplication it is then to get the answer of 1 6/2(1+2) 6/2(3) 6/6 1 it still follows PEMDAS @Kosmonaut here is my take to get that 1 answer that it follows PEMDAS still we need @Meusnier on this thread lol @Kosmonaut @AlexPaulLEWZ Just quoting those who said interesting things. PEMDAS, DMAS, BIDMAS, BODMAS, all this nonsense is still taught these days? The answer was in the question. The notation is wrong and what is written is meaningless. Amusing to see people insulting each other about something they are manifestly clueless about. As Alex said, you can only write 6/(2(1+2)) or (6/2)(1+2), and 6/2(1+2) is incorrect. People argue over left versus right, or division against multiplication, but multiplication and division is the same thing, and the multiplication is commutative, that is: a ⋅ b=b ⋅ a. Besides schoolboys, no one writes /, unless someone writes 1/3 or f/g, with f,g two given functions. The solution to avoid confusion is to add the exponent -1 for the inverse, and to always write expressions of the form: 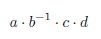 and never expressions of the following form:  This is not about being pedantic, all signs have a meaning, and if one is missing, the entire expression may stop to make sense; by the way, this is exactly the same thing to leave the possibility of distinct explanations for the reader and being meaningless. Using calculators and computers has nothing to do with the argument here as they are designed to satisfy some arbitrary conventions. They do not constitute anything reliable. Rather than believing inept teachers, one should rather look back at the axioms of fields. Those are sets X equipped with too operations, + and ⋅, for which there exists distinct elements 0, 1∈X, such that x+0=x and x ⋅ 1=x for all x∈X, and such that for all for all x∈X, there exists y∈X such that x+y=0. We note y=-x. We also require that for all x∈X different from 0, there exists y∈X such that x ⋅ y=1. We write  . .Then the only axioms satisfied by the field X are the following :
In particular, there is nothing saying you should compute anything from left to right or right to left. One has to make a difference between an inconvenient rule taught to children so that they make less computational mistakes and what one can actually rightfully do according to the axioms. @Kosmonaut Feel free to call me Neo from now. Now we all know what is being redpilled, it means being able to understand basic mathematical axioms. @Phloup Needless to say, I disagree with your post. Still, I can't help but feel like my high school math teacher would be proud of me for turning a division into a multiplication, after so many years, even if I was wrong. I'll take solace in the little redpills, while you've already become big pharma. I also think that this is the main point of all this, to trick the reader into thinking that there is a solution by being imprecise on notations. Certainly, a teacher should never write such questions in an exam. You may find however people who write papers with such shaky notations, but their existence does not mean that it is fine to do that. Indeed, and this is why people are so annoying with parenthesis at school, for one easily writes things subject to interpretation, i.e. false. Well, still better that this guy I saw writing inequalities between complex numbers at the exam to become a high school teacher. If you want to have fun hearing about wrong mathematical writing, I would recommend this video of Serre. |
Nov 17, 2020 4:07 PM
#67
Nov 17, 2020 4:14 PM
#68
Meusnier said: The answer was in the question. The notation is wrong and what is written is meaningless. Amusing to see people insulting each other about something they are manifestly clueless about. As Alex said, you can only write 6/(2(1+2)) or (6/2)(1+2), and 6/2(1+2) is incorrect. People argue over left versus right, or division against multiplication, but multiplication and division is the same thing, and the multiplication is commutative, that is: a ⋅ b=b ⋅ a. Besides schoolboys, no one writes /, unless someone writes 1/3 or f/g, with f,g two given functions. The solution to avoid confusion is to add the exponent -1 for the inverse, and to always write expressions of the form: 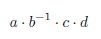 and never expressions of the following form:  This is not about being pedantic, all signs have a meaning, and if one is missing, the entire expression may stop to make sense; by the way, this is exactly the same thing to leave the possibility of distinct explanations for the reader and being meaningless. Using calculators and computers has nothing to do with the argument here as they are designed to satisfy some arbitrary conventions. They do not constitute anything reliable. Rather than believing inept teachers, one should rather look back at the axioms of fields. Those are sets X equipped with too operations, + and ⋅, for which there exists distinct elements 0, 1∈X, such that x+0=x and x ⋅ 1=x for all x∈X, and such that for all for all x∈X, there exists y∈X such that x+y=0. We note y=-x. We also require that for all x∈X different from 0, there exists y∈X such that x ⋅ y=1. We write  . .Then the only axioms satisfied by the field X are the following :
In particular, there is nothing saying you should compute anything from left to right or right to left. One has to make a difference between an inconvenient rule taught to children so that they make less computational mistakes and what one can actually rightfully do according to the axioms. @Phloup Needless to say, I disagree with your post. After reading your post, and looking at the equation again, I completely see the flaws in my initial post. Although I may seem like on of these people who immediately agrees with someone else if they sound smart, I understand where I went wrong with my thinking. So, if I understand correctly, this equation was simply written poorly, which would cause misinterpretation to happen easily. I fully agree on that the use of slashes for fractions can easily cause confusion with the equation, which is one of the limitations of writing on a keyboard. Also, personal thoughts of mind: I personally would rather use fractions instead of exponents (for an inverse value) and I find the division sign to be a potential catalyst for misinterpretation. |
Nov 17, 2020 4:25 PM
#69
| All the posts and paragraphs were for nothing, rip. |
 Leading biologist Scott Pitnick said: The bigger your 'nads, the smaller your brains |
Nov 17, 2020 4:25 PM
#70
| PEMDAS should be the method that needs to be used in this problem: The answer is obviously 1. 6/2(1+2) = 6/2(3) P - Parenthesis 6/2(3) E - Exponent 6/2(3) = 6/6 M - Multiplication 6/6 = 1 D - Division 1 A - Addition 1 S - Subtraction Therefore, the answer is 1 The problem is not confusing. |
-Kazuma_Nov 17, 2020 4:33 PM
| Signature removed. Please follow the signature rules, as defined in the Site & Forum Guidelines. |
Nov 17, 2020 4:32 PM
#71
Nov 17, 2020 4:37 PM
#72
Eren_Midoriya said: PEMDAS should be the method that needs to be used in this problem: The answer is obviously 1. 6/2(1+2) = 6/2(3) P - Parenthesis 6/2(3) E - Exponent 6/2(3) = 6/6 M - Multiplication 6/6 = 1 D - Division 1 A - Addition 1 S - Subtraction Therefore, the answer is 1 The problem is not confusing. Multiplication does not precede division. For example, some people are taught BODMAS or BEDMAS. |
Nov 17, 2020 4:40 PM
#73
Nov 17, 2020 4:50 PM
#74
Opticflash said: Eren_Midoriya said: PEMDAS should be the method that needs to be used in this problem: The answer is obviously 1. 6/2(1+2) = 6/2(3) P - Parenthesis 6/2(3) E - Exponent 6/2(3) = 6/6 M - Multiplication 6/6 = 1 D - Division 1 A - Addition 1 S - Subtraction Therefore, the answer is 1 The problem is not confusing. Multiplication does not precede division. For example, some people are taught BODMAS or BEDMAS. Multiplication can precede division. As a matter of fact, PEMDAS is more commonly use than BEDMAS. |
| Signature removed. Please follow the signature rules, as defined in the Site & Forum Guidelines. |
Nov 17, 2020 4:51 PM
#75
| Soo the answer is there is no correct answer |
| "Rating are for Casul" "While masterpiece are for Pleb" "But shit taste is enlightenment" "Go watch School Days you Weebs" |
Nov 17, 2020 5:04 PM
#76
Eren_Midoriya said: Opticflash said: Eren_Midoriya said: PEMDAS should be the method that needs to be used in this problem: The answer is obviously 1. 6/2(1+2) = 6/2(3) P - Parenthesis 6/2(3) E - Exponent 6/2(3) = 6/6 M - Multiplication 6/6 = 1 D - Division 1 A - Addition 1 S - Subtraction Therefore, the answer is 1 The problem is not confusing. Multiplication does not precede division. For example, some people are taught BODMAS or BEDMAS. Multiplication can precede division. As a matter of fact, PEMDAS is more commonly use than BEDMAS. Perhaps in the US, and which is why the answer is not obviously 1. In addition if you use any sort of computational software that mathematicians, scientists and engineers use (Matlab, Wolfram Alpha, Mathematica, etc.) in ordinary practise, the agreed convention for these sorts of calculations would result in a 9 for the question given. Of course if you're writing an equation or expression in say an academic paper, you should aim to make your meaning clear by placing more parentheses where appropriate. |
Nov 17, 2020 10:44 PM
#77
| It's mostly likely 1. That's what I found using the BEDMAS method, at least. |
Nov 18, 2020 12:44 AM
#78
Nov 18, 2020 7:41 AM
#79
| Thank you lord @Meusnier Solving equations from left to right is one of the dumbest thing I've ever heard concerning mathematics. I've also never understood why someone would unnironically write ÷2 instead of x0.5 As a side note, I've seen this format of equation in one of my math textbook e.g 6/2*3=1 It was written like that to save room instead of writing the whole fraction, but there was a notice at the bottom telling that the slash is meant to separate all the numerator from the left and all the denominator from the right. It found it quite practical as it avoids writing unnecessary brackets and exponent -1. Is this nomenclature frequently used in math textbook? |
Nov 18, 2020 9:14 AM
#80
| 9 assuming you know the basic rules of pemdas, and solve left to right though 1 can be correct since this a poor way to write the equation to begin with because of how easily it can be misinterpreted. Also damn lol, the two "most correct" answers are neck and neck that's pretty cool. |
| youtube.com/watch?v=oHg5SJYRHA0 73 6f 6d 65 74 68 69 6e 67 73 20 6f 64 64 20 61 62 6f 75 74 20 6d 79 20 70 72 6f 66 69 6c 65 0d 0a |
Nov 18, 2020 9:24 AM
#81
| This is actually pretty easy 6 : 2(1+2) 6 : (2+4) 6 : 6 1 |
 |
Nov 18, 2020 3:11 PM
#82
| Didn't notice the 6: was part of the question because : don't indicate a division sign |
Nov 18, 2020 3:41 PM
#83
| There will be a free drink distribution festival. Every day that I go to the festival, I will get a constant of one bottle of water plus two bottles of coke. However, on the second day, this total will be multiplied by two. On the third day, in addition to the constant plus the multiplication, there will be a division of the result. If the result is less than one bottle of each, you'll just get a coke. On the fourth day, the festival ends. What is the end result? Day 1: 2 bottles of water + 1 coke Day 2: 4 bottles of water + 2 cokes Day 3: 6:2x(1+2) -> 1, so, as the rule says, you'll only get 1 bottle of coke. Total on day 4: 6 bottles of water, 4 bottles of coke. Change my mind. |
Nov 18, 2020 4:34 PM
#84
Nov 18, 2020 4:36 PM
#85
| Oh shit. It's 3x3 = 9. Why a few do something different? |
| BANZAI NIPPON. Nippon is the Land of freedom. Nippon is the Land of Peace. Nippon is the Land of Justice and Prosperity. In Nippon, we trust. We love Nippon, we love Anime. Anime love us, Nippon love us. 日本 I believe in freedom of expression. |
Nov 18, 2020 5:31 PM
#86
| 9 6 ÷ 2(2+1) = 6 ÷ 2(3) which is the same as 6 ÷ 2 x 3 = 3 x 3 = 9 according to the standard DMAS rule. |
  Look at the stars, they are retreating. |
Nov 18, 2020 10:59 PM
#87
| Probably 9 by BODMAS Add the numbers in the bracket ( ), divide 6 by 2. You will get 3×(3). Its 9 |
Nov 18, 2020 11:32 PM
#88
| Going by BODMAS, the answer is 9. 6/2(1+2) 6/2(3) 3.3 9 |
Nov 19, 2020 11:30 AM
#89
Nov 19, 2020 11:40 AM
#90
| I HEARBY SUMMON THE POWER OF PEMDAS 6 / 2(1+2) P (parenthesis) - 3 6 / 2 (3) Multiplication - 6 6 / 2*3 = 6 Division - 6/6 = 1 COINCIDENCE? I THINK NOT! |
Nov 19, 2020 11:41 AM
#91
| my answer 9, grouped operation first, then i believe that multiplication and division have the same priority and the ordering takes over, so the left one goes first |
Nov 19, 2020 12:49 PM
#92
rudnam said: my answer 9, grouped operation first, then i believe that multiplication and division have the same priority and the ordering takes over, so the left one goes first They have the same priority, yet you decided a certain order takes over? |
Nov 19, 2020 1:00 PM
#93
Phloup said: Meusnier said: The answer was in the question. The notation is wrong and what is written is meaningless. Amusing to see people insulting each other about something they are manifestly clueless about. As Alex said, you can only write 6/(2(1+2)) or (6/2)(1+2), and 6/2(1+2) is incorrect. People argue over left versus right, or division against multiplication, but multiplication and division is the same thing, and the multiplication is commutative, that is: a ⋅ b=b ⋅ a. Besides schoolboys, no one writes /, unless someone writes 1/3 or f/g, with f,g two given functions. The solution to avoid confusion is to add the exponent -1 for the inverse, and to always write expressions of the form: 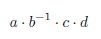 and never expressions of the following form:  This is not about being pedantic, all signs have a meaning, and if one is missing, the entire expression may stop to make sense; by the way, this is exactly the same thing to leave the possibility of distinct explanations for the reader and being meaningless. Using calculators and computers has nothing to do with the argument here as they are designed to satisfy some arbitrary conventions. They do not constitute anything reliable. Rather than believing inept teachers, one should rather look back at the axioms of fields. Those are sets X equipped with too operations, + and ⋅, for which there exists distinct elements 0, 1∈X, such that x+0=x and x ⋅ 1=x for all x∈X, and such that for all for all x∈X, there exists y∈X such that x+y=0. We note y=-x. We also require that for all x∈X different from 0, there exists y∈X such that x ⋅ y=1. We write  . .Then the only axioms satisfied by the field X are the following :
In particular, there is nothing saying you should compute anything from left to right or right to left. One has to make a difference between an inconvenient rule taught to children so that they make less computational mistakes and what one can actually rightfully do according to the axioms. @Phloup Needless to say, I disagree with your post. After reading your post, and looking at the equation again, I completely see the flaws in my initial post. Although I may seem like on of these people who immediately agrees with someone else if they sound smart, I understand where I went wrong with my thinking. So, if I understand correctly, this equation was simply written poorly, which would cause misinterpretation to happen easily. I fully agree on that the use of slashes for fractions can easily cause confusion with the equation, which is one of the limitations of writing on a keyboard. Also, personal thoughts of mind: I personally would rather use fractions instead of exponents (for an inverse value) and I find the division sign to be a potential catalyst for misinterpretation. Indeed, both interpretations are correct, as / can notably be seen as the inverse function (see below), and this is why some math majors here interpreted it as an expression equating to 1. When dealing with real numbers, I also agree that this is much better to use horizontal fraction signs, unless one writes 1/5 and does not want a change of spacing of lines. Hrybami said: Thank you lord @Meusnier Solving equations from left to right is one of the dumbest thing I've ever heard concerning mathematics. I've also never understood why someone would unnironically write ÷2 instead of x0.5 As a side note, I've seen this format of equation in one of my math textbook e.g 6/2*3=1 It was written like that to save room instead of writing the whole fraction, but there was a notice at the bottom telling that the slash is meant to separate all the numerator from the left and all the denominator from the right. It found it quite practical as it avoids writing unnecessary brackets and exponent -1. Is this nomenclature frequently used in math textbook? Indeed, if I ask 61×51/3, I hope that people will not do that from left to right. Thank you for your question, it will allow me to speak about something else of importance. I have not seen this convention applied much, maybe more in the physics literature? g(x,y,z)/f(x,y,z) is common though. However, one can interpret / as the inverse function, and in general, on does not need to write parenthesis in this case to indicate that it applies to all variables. For example, writing 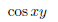 should always be interpreted as  and not as  If one means the above notation, one can also do without parenthesis to be sure that typos will not make things unclear to the reader 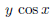 This being said, the notation above should not be encouraged in general. Of course, there are no confusions possible with exponents.  To give another example of style, this notation 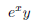 is acceptable but this one 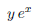 seems more readable to me and the following may be used too 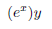 There is a delicate balance to find between clarity and number of parenthesis! |
Nov 19, 2020 1:25 PM
#94
| @Meusnier Thank you for pointing this out. I find this quite funny since every sub category of science (math, physicist, chemist, biologist, etc.) use more or less their own conventions. It happened to me when I read something from a different scientific field and was confused over their odd conventions. But it makes sense since they don't work and study in the same area and some things are to be taken into consideration. However, I think we would all agree that a formula absolutely need to be clear and without ambiguity. |
Nov 19, 2020 1:29 PM
#95
Hrybami said: @Meusnier Thank you for pointing this out. I find this quite funny since every sub category of science (math, physicist, chemist, biologist, etc.) use more or less their own conventions. It happened to me when I read something from a different scientific field and was confused over their odd conventions. But it makes sense since they don't work and study in the same area and some things are to be taken into consideration. However, I think we would all agree that a formula absolutely need to be clear and without ambiguity. You are very welcome! Indeed, reading the physics literature always feels a bit unpleasant to me due to their strange notations with a lot of indices and the reverse order of variables in integrals notably. But the most important thing is that people know about the conventions, while in this problem, people merely guess them. |
Nov 19, 2020 1:42 PM
#96
Meusnier said: Hrybami said: @Meusnier Thank you for pointing this out. I find this quite funny since every sub category of science (math, physicist, chemist, biologist, etc.) use more or less their own conventions. It happened to me when I read something from a different scientific field and was confused over their odd conventions. But it makes sense since they don't work and study in the same area and some things are to be taken into consideration. However, I think we would all agree that a formula absolutely need to be clear and without ambiguity. You are very welcome! Indeed, reading the physics literature always feels a bit unpleasant to me due to their strange notations with a lot of indices and the reverse order of variables in integrals notably. But the most important thing is that people know about the conventions, while in this problem, people merely guess them. Indeed I know how you feel. You're talking about the problem of this thread? I don't think people guess anything. They applied what they were taught back when they were 12 without thinking twice. I mean just the fact that there is a ÷ symbol should ring some bells that this problem is potentially horribly written. |
Nov 19, 2020 3:32 PM
#97
Hrybami said: Meusnier said: Hrybami said: @Meusnier Thank you for pointing this out. I find this quite funny since every sub category of science (math, physicist, chemist, biologist, etc.) use more or less their own conventions. It happened to me when I read something from a different scientific field and was confused over their odd conventions. But it makes sense since they don't work and study in the same area and some things are to be taken into consideration. However, I think we would all agree that a formula absolutely need to be clear and without ambiguity. You are very welcome! Indeed, reading the physics literature always feels a bit unpleasant to me due to their strange notations with a lot of indices and the reverse order of variables in integrals notably. But the most important thing is that people know about the conventions, while in this problem, people merely guess them. Indeed I know how you feel. You're talking about the problem of this thread? I don't think people guess anything. They applied what they were taught back when they were 12 without thinking twice. I mean just the fact that there is a ÷ symbol should ring some bells that this problem is potentially horribly written. Yes, I was still talking about the problem of this thread. You are probably right that people apply the rules like some recipes they would have learned from their parents. |
Nov 19, 2020 3:53 PM
#99
This problem was written about ad nauseum months ago and everyone basically concluded that the statement itself is vague, causing people to arrive to two correct answers:
The issue is various software packages or calculators would solve multiplication by parentheses (as opposed to "x") first, considering them the same term, or the division symbol (as opposed to "/") last. In real life, no one mixes the division symbol while eliminating the "x". And if it's ambiguous, usually mathematicians would clarify. The point of math is communication, not to trick you with gotchas. But if you want to answer this properly by how they taught you in high school, then the answer would be 9. |
| My subjective reviews: katsureview.wordpress.com THE CHAT CLUB. |
Nov 19, 2020 9:08 PM
#100
Hrybami said: rudnam said: my answer 9, grouped operation first, then i believe that multiplication and division have the same priority and the ordering takes over, so the left one goes first They have the same priority, yet you decided a certain order takes over? i meant that since it's pemdas (implies multiplication before division, but actually same prio, ordering takes over) |
More topics from this board
» What is the last compliment you received on MAL? (By who?)Tamim1357 - Oct 26 |
11 |
by Retro8bit
»»
6 minutes ago |
|
» would you be able to forgive your bullies if they apologized?Ymir_The_Viking - Oct 25 |
25 |
by Retro8bit
»»
6 minutes ago |
|
» Where do you guys meet people irl?Cneq - Oct 25 |
18 |
by Retro8bit
»»
7 minutes ago |
|
» In which country do you think nature is least likely to kill you?fleurbleue - Oct 24 |
21 |
by Retro8bit
»»
8 minutes ago |
|
» Would you go Trick-or-Treating with your avatar/signature on Halloween?IpreferEcchi - Oct 25 |
12 |
by Retro8bit
»»
8 minutes ago |















